均质滤料过滤过程的毛细管去除浊质模型
景有海1，金同轨1，范瑾初2
（1.西安建筑科技大学 环境与市政工程学院，陕西 西安 710055；2.同济大学 环境科学与工程学院，上海 200092）
摘要：通过将粒状材料组成的滤床抽象为由无数条毛细管道组成的管束，将过滤过程描述为水流在毛细管道中流动时的管壁吸附过程，从而推导出了均质滤料过滤过程的浊质去除数学模型。
关键词：均质滤料；过滤过程；毛细管模型；过滤方程
中图分类号：TU991.24
文献标识码：A
文章编号：1000-4602(2000)06-0001-04
Capillaries Model for Turbidity Removal in Filtration Process with Uniform Media
JING You hai1，JIN Tong gui1，FAN Jin chu2
(1.School of Environ. and Munic. Eng., Xi‘an Univ. of Architec. and Tech., Xi’an 710055,China; 2.School of Environ.Sci.and Eng.,Tongji Univ.,Shanghai 200092, China)
? Abstract：based on simulating the granular filter bed as tubes formed by numerous cylindrical capillaries, this paper described filtration tube wall adsorption process when water was flowing in capillaries. results, a mathematical model of turbidity removal with uniform media deduced.?
Keywords: uniform media;filtration;capillaries model;filtration equation
基金项目： 国家自然科学基金资助项目(59778022)
1.均质滤料过滤过程的毛细管模型
由粒状材料组成的滤床，内部有无数孔隙通道。水流通过滤层的过滤过程，就是水流在滤床孔隙内的流动过程。因此，可将滤床看成是有无数条毛细管道组成的管束，过滤过程就是水流在这些毛细管道中的流动过程。为了使水流在毛细管道中的过滤条件与实际滤床中的过滤条件相同，必须具备以下两个条件：
① 毛细管道的总空间应与滤床的孔隙相同；
② 毛细管道的总表面积应与滤料的表面积相同。
假设滤池面积为F(m2)，滤床深度为L(m)，滤料的孔隙率为ε(m3孔隙/m3滤料)，滤料的比表面积为f(m2表面/m3滤料)；并假设单位面积滤池拥有毛细管数量为n(根/m2滤池)，毛细管的管径为dm(m)。因此，根据上述两条原则，将均质滤料滤床描述为毛细管模型时，必须满足下列两个等式：
ε＝n·πdm2/4 (1)
f＝n·πdm (2)
对于非球形级配滤料，其比表面积可表示为：
f=6α(1-ε)/de (3)
式中 α——滤料的表面形状系数
de——滤料的当量直径，m
联解式（1）和式（2），并将式(3)代入可得：
dm=2εde/(3α(1-ε)) (4)
n=9α2(1-ε)2/πεde (5)
此即为笔者将滤池抽象为毛细管模型时的毛细管管径和单位面积滤池拥有毛细管数量的计算公式。
2 过滤过程的浊质去除计算模型
取滤层中某一毛细管作为考查对象，在滤层深度z处取断面1，并在深度z+dz处取断面2，如图1所示。
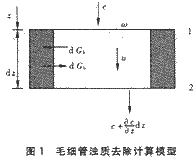
假设在时刻t,断面1处的浊质浓度为c，过流断面面积为ω，沉积在毛细管壁单位管长上的浊质体积量为σd(m3浊质/m管长），滤层的浊质比沉积量为σd(m3浊质m3滤料），则有：
σd=σ/n （6）
断面2处的浊质浓度为：
，经过dt时段后，dz长度毛细管壁上的浊质增加量为：
水中浊质因被毛细管壁吸附后，其管壁附近浊质浓度降低，使得毛细管中心浊质与管壁附近出现浓度梯度。在浓度梯度的推动下，管中心浊质向管壁扩散，这种扩散包括面朗运动扩散和水力扩散。
式中 D——浊质的扩散系数，m2/s
rm——毛细管壁吸附浊质后的孔道半径，m
因此，经dt时段的扩散量即沉积量为：
沉积在毛细管壁上的浊质，因水流的剪切力而被剥落下来，其剥离速率可认为与水流的剪切力和毛细管道的堵塞率成正比，即：
式中 B——浊质的剥离系数，m3/(N.s），与滤料的表面特性以及水中浊质颗粒的表面特性即混凝特性有关。混凝效果好，B值小，否则B值大。采用高分子混凝剂时，其B值就远小于采用硫酸铝作混凝剂时的B值
τ——水流的剪切应力，N/m2
μ——水的动力粘性系数，Pa.s
则其剥离量为：
式（12）即为本文作者推导出的均质滤料过滤过程的滤层堵塞方程式，式中滤速v的单位为m/s。
在滤层中取一毛细管作为考查对象，如图2所示。由表层算起，毛细管长管为z，进入毛细管的浊质浓度为c0，从毛细管流出的浊质浓度为c。过滤从时间0开始，经过时段t过滤后，毛细管单位长度上的浊质吸附量σd，根据物料平衡有：
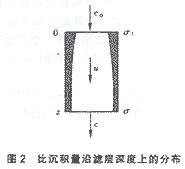
式（14）即为本文作者推导出的均质滤料过滤过程的连续性方程。式中c为过滤流体中的浊质何种浓度，其单位为（m3固体/m3液体）。显然，c的最大值为1。当c=1时，表示过滤介质变为固体。在一般的流体过滤过程中，其注质浓度c＜＜1，则上式可简化为：
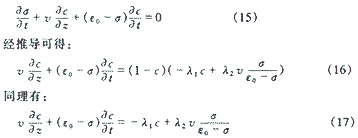
式（16）和式（17）即为本文作者推导出的均质滤料过滤过程的毛细管去除浊质计算模型，即过滤方程。由式（12）和式（17）可以看出：当进水浊质浓度c=0、比沉积量σ≠0时，浊质的去除速率为正值，而比沉积量的沉积速率为负值。这说明水中浊质浓度增加，而比沉积量减小，它正好描述了反冲洗时的滤层清洁过程。因此式（12）、（15）和（17）不仅是过滤方程，同时也是滤层在不扰动情况下的反冲洗方程，这正好说明反冲洗过程是过滤过程的逆过程。
3 过滤方程式的简化分析
方程（12）、（15）和（17）中，σ和c均为滤层深度z和过滤时间t的函数，即：
σ=σ（z，t) （18）
c=c(z,t） （19）
显然，上述方程为二元二次函数一阶非线性方程组，目前还难以求得其精确的解析解。现对其进行简化分析和近似解答，更精确的解答要通过数值分析来求得。
3.1 滤层中的最大比沉积量
对于滤层堵塞方程式（12），当滤层截留浊质达到饱和时，有：
3.2 滤层失去除浊能力时所需过滤时间
对于滤层表层，当z=0时，有c=c0=常数，此时，滤层堵塞方程（12）变为：
dσi/dt=λ1c0-λ2[σi/(ε0-σi)]υ （25）
上式中，σi为z=0时的滤层比截污量。对止式积分并设过滤是从清洁滤层开始，当t=0时，σi=0，则有：
t=（λ2υε0/φ）ln[λ1υε0/（λ1υε0-φσi）+σi/φ （26）
当滤层即将失去除浊能力时，有σi→σmax=λ1υε0/φ，此时所需要的过滤时间为：
也就是说，在有限的过滤时间内，理论上滤层难以达到完全饱和，这在过滤试验中已基本得到证实。因此，在实际应用中，当σ=95%σmax时，即可认为滤层已达到饱和状态。此时所需要的过滤时间为：
3.3 滤层沿深度方向的比沉积量分布规律
由滤层堵塞方程，因σ/（ε0-σ）=u，得到：
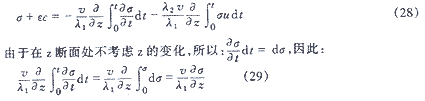
对于式（28）右边第二项，由于udt=dz，且有当t=0时z=z当t=t时z=z’，其z’为假设毛细管为无限长时，经过t时间段后，流体沿毛细管流行的距离，因此有
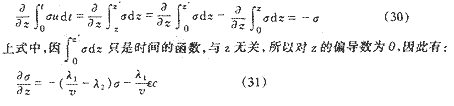
式（31）即为比沉积量沿滤层深度方向上的分布规律。
由式（12）和式（31）可得：
式中σi为滤层表层z=0处的比沉积量，它满足方程（26）。由此可见，σ是过滤时间t和滤层深度z的函数。
由式（33）可以看出，在过滤过程中，滤层中的比沉积量沿深度方向近似按负指数规律衰减。提高滤速，则比沉积量衰减率减小，浊质向滤层深处穿透，比沉积量在滤层中的分布趋于均匀。混凝效果提高，λ2减小，比沉积量衰减率增大，表明浊质较易被表层截留。
由式(31)可以看出，
不可能为0(除非λ1＝λ2＝0)。因此，严格讲滤层中不可能出现饱和阶段。否则，从函数连续性角度考虑，比沉积量沿深度方向的变化必然出现拐点。但因其分布近似于负指数规律，不可能有拐点。另一方面，假如滤层中有饱和层出现，那么该滤层中将不会再有浊质截留，该段滤层的水头损失也将不会再随过滤时间的延长而增大。但在过滤试验中并未发现这样的阶段出现。因此可以说，在过滤过程中，滤层中不可能有饱和阶段出现。
4 结论
① 将均质滤料滤池描述为毛细管模型有助于简化过滤过程的分析，其结论仍然可用。
② 在有限的过滤时间内，严格讲，滤层中不可能出现饱和阶段。
③ 滤层中的比沉积量近似按负指数规律分布。
参考文献：
［1］许保玖，安鼎年.给水处理理论与设计［M］.北京：中国建筑工业出版社，1992.
［2］严熙世，范瑾初.给水工程［M］.北京：中国建筑工业出版社，1995.
［3］Ю·M·康士坦丁诺夫.水力学［M］.钟用升译.江西高校出版社，1990.
作者简介：景有海(1962-)，男，陕西陇县人，西安建筑科技大学副教授，硕士，主要从事水处理技术方面的教学和科研工作。
电话：(029)5234941
收稿日期：2000-01-23
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时，试验有了起色时，是不是想和同行探讨一下，工作中有了心得，您是不是很想与人分享，那么不要只是默默工作了，写下来吧！投稿时，请以附件形式发至 paper@h2o-china.com ，请注明论文投稿。一旦采用，我们会为您增加100枚金币。
