迭代方法在明渠水力计算中的应用
樊建军,刘金香,袁华山
(南华大学建筑工程与资源环境学院,湖南衡阳421001)
摘 要:为克服明渠水力计算中试算法带有盲目性、计算工作量大和图解法使用不便、精度较差的缺陷,在对明渠水力计算公式进行充分剖析的基础上,给出了相应的迭代公式,并从数学上证明了迭代公式的收敛性。公式用于工程设计计算具有速度快、精度高的优点,效果令人满意。
关键词:迭代法;明渠;水力计算
中图分类号:TU991.32
文献标识码:C
文章编号:1000-4602(2001)06-0043-02
1 基本公式与迭代公式
明渠均匀流的基本公式为:
![]()
式中 Q——流量
i——渠道底坡
n——粗糙系数
m——边坡系数
b——渠底宽度
h——水深
对基本公式加以改造,可得求解b或h的迭代公式:
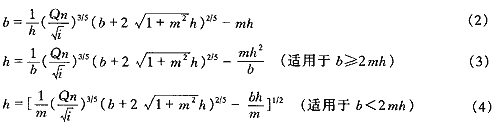
明渠水流处于临界流状态时,各参数满足以下关系:
αQ2/g=(b+mhk)3hk/b+2mhk (5)
式中 α——动能修正系数,通常取α=1
g——重力加速度
hk——临界水深
对式(5)进行改造,可得计算临界水深的迭代公式:
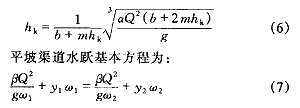
式中 β——动量修正系数,通常取β=1
ω——过水断面面积,ω=(b+mh)h
y——过水断面形心水深,y=3bh+2mh2/6(b+mh)
令θ(h)=βQ2/gω+yω,用h′与h″分别代表跃前水深与跃后水深,由水跃基本方程可导出以下迭代公式:
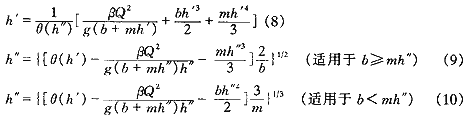
2 收敛性证明
根据迭代理论,假设方程f(x)=0的一个根为a,若把f(x)=0变形为x=φ(x),则迭代形式xn+1=φ(xn)收敛于a的条件是,如果在a的某一邻域|x-a|<δ内,|φ′(x)|<1,那么以该邻域内任一点为初值的迭代都收敛于a。
下面以迭代式(2)为例,证明其收敛性,其他迭代式都可用同样方法得到证明。
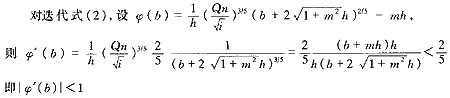
3 迭代初值的确定及实例计算
虽然迭代式(2)、(3)、(4)、(6)、(8)、(9)、(10)对公式适用范围内的任意初值均收敛,但初值选取是否恰当对迭代计算工作量有一定影响。通过深入分析迭代公式各参数间的关系,建议对迭代式(2)、(3)、(4)、(6)均取初值为零,对迭代式(8)、(9)、(10)则分别取初值如下:
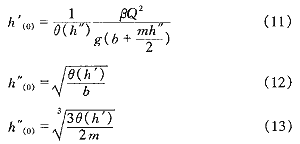
实例计算:
例1,有一梯形渠道,采用小片石干砌护面(n=0.02),设计流量Q=10m3/s,m=1.5,i=0.003,要求水深h=1.5 m,试确定渠底宽度b。
解:用迭代式(2)计算,取初值b(0)=0,可求得b(1)=0.60,b(2)=0.72,b(3)=0.75,b(4)=0.75。
取渠底宽度为0.75 m。
例2,有一梯形渠道,用大块石干砌护面(n=0.02),已知b=7 m,m=1.5,i=0.001 5,需要通过流量Q=18 m3/s,试确定渠道的正常水深h。
解:初估水深<2 m,则b>2 mh,可用迭代式(3)计算,取初值h(0)=0,代入式(3)可求得h(1)=1.19,h(2)=1.13,h(3)=1.15,h(4)=1.14。
取正常水深为1.14 m。
例3,有一梯形断面小河,b=10 m,m=1.5,Q=30m3/s,试确定临界水深。
解:用迭代式(6)计算,取初值hk(0)=0,可求得hk(1)=0.972,hk(2)=0.924,hk(3)=0.926,hk(4)=0.926。
取hk=0.926 m。
例4,某梯形渠道,b=7 m,m=1,Q=54.3m3/s,渠中有水跃发生,已知h′=0.8 m,试确定h″。
解:初估h″<7 m,则b>mh″,可用迭代式(9)计算。

4 结语
实例计算表明,文中给出的迭代方法相对于目前采用的试算法和图解法而言,既减少了计算工作量,又提高了计算精度,不失为工程设计计算的好方法。
虽然求解正常水深和跃后水深的迭代公式均有两个,但根据具体问题和计算者的实践经验,很容易确定采用哪一个迭代式,即使起初无法判断,也只需经过一次迭代后就能作出正确判断,使用也是方便的。
因迭代计算是简单的重复,经常从事明渠水力计算的工作人员可编制迭代计算程序,采用计算机运算,一劳永逸。
参考文献:
[1]清华大学水力学教研室编.水力学[M].北京:人民教育出版社,1980.
[2]成都科学技术大学水力学教研室编.水力学(上册)[M].北京:人民教育出版社,1979.
[3]武汉大学,山东大学编.计算方法[M].北京:人民教育出版社,1979.
电 话:(0734)8282020
收稿日期:2000-11-21
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 paper@h2o-china.com ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








