灰色关联模型用于工程方案优化

王浙明1， 史惠祥2， 苏雨生1， 汪大翬2
( 1.浙江省环境保护科学设计研究院，浙江杭州310007；2.浙江大学环境工程研究所，浙江杭州310027)

　　摘　要：针对目前在城市污水处理厂的可行性方案比较和选择中，存在主观随意性较大的问题，将模糊数学中的灰色关联分析法与工程优化中多目标决策思想相结合，建立了城市污水处理厂工程方案优化的灰色关联多目标决策模型，并对模型中的评价指标引入了权重的概念。该模型应用于钱塘江流域某城市污水处理厂工程方案的优化选择，取得了较为满意的效果。
　　关键词：灰色关联；多目标决策；优化模型；污水处理厂
　　中图分类号：X505
　　文献标识码：C
　　文章编号： 1000-4602(2002)01-0081-04

　　在当前城市污水处理厂可行性研究中，由于还没有形成一整套工艺选择的评判方法，在方案比较和选择时主要凭概算得到的费用和方案设计人对各工艺方案的主观认识进行，因此存在较大的主观随意性。城市污水处理厂工艺选择涉及的影响因素较多，如当地政府财政的承受能力、城市附近水体及流域对除磷脱氮的要求、是否需要考虑处理水回用及各工艺方案的成熟度等，为此应用模糊数学中的灰色关联分析法和工程优化中多目标决策思想建立城市污水处理厂工程方案的优化模型，并对评价指标引入权重的概念以与城市污水处理厂的实际相符合，旨在形成一套客观的工程方案优化方法。

1 模型的建立

1.1 确定指标特征量矩阵
　　工程项目可行性研究中多方案优化选择问题就是有限个方案的多目标决策问题。设系统由m个待选方案组成，记为Ai(i=1，2，…，m)；各方案又有n个评价指标组成评判方案优劣的指标集，记为aj(j=1，2，…，n)。据此，可以得到m个方案的指标特征量矩阵(也称决策矩阵)：

　　

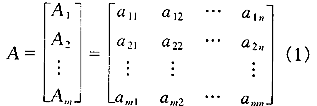
1.2 理想方案的确定
　　理想方案是客观上可能出现的最好方案，它不在n个投标方案中产生，而是根据这类方案的性质、设计能力以及各指标在过去曾出现和将来可能或希望出现的最优值而定的，是从投标方案的外界产生的。
　　设理想方案为：

　　A0=(a01a⁰2…a⁰n)

　　由此构成(m+1)个方案的指标特征量矩阵：

　　

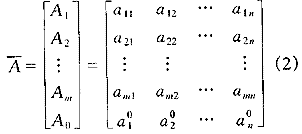
1.3 特征量矩阵的规范化
　　在城市污水治理工程方案的评价指标中，基建投资、年运行费用、占地面积等是属于愈小愈好的成本型指标；而工艺技术、操作管理、出水稳定性及除磷脱氮等则属于愈大愈好的效益型指标。这些指标往往具有不同的量纲，且数值间差异较大。为消除它们对决策结果的影响，需要对指标特征量矩阵A作规范化处理，转化为规范化矩阵S。又由于成本型指标和效益型指标在采用线性变换的规范化方法时所采用的基点不同，会使变换后最好的效益目标和成本目标有不同的值，不便于比较。因此采用下式对A进行规范化处理。
　　对于效益型指标，令：
　　　　　　sij=aij／a⁰j　　　　(3)
　　对于成本型指标，令：
　　　　　　sij=a⁰j／aij　　　　(4⁾
　　(3)、(4)两式中，aij为决策矩阵中第i个待决策方案的第j项指标的实际值。显然，0≤sij≤1，且sij的值越大方案越优。因此，A 的规范化矩阵为：

　　

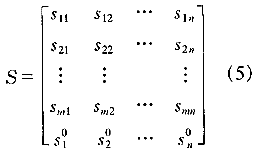
1.4 指标权重的确定
　　由专家对工程方案的评价指标aj(j=1，2，…，n)进行两两比较，由比较的结果确定其判断矩阵B：

　　

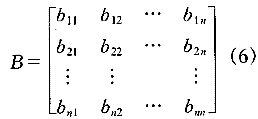
　　设评价指标a1、a2、…、an的权重为w=［w1w2 …wn］，应用权的最小平方法有：
　　　　　CwT=m　　　　　　　　(7)
　　式中： m=［-λ-λ…-λ］T

　　

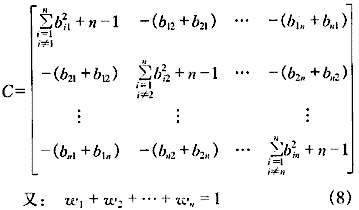
　　权重w和系数λ即可由式(7)、(8)求得。
1.5 关联系数的计算
　　根据灰色关联分析法，待决策方案Ai的决策矩阵Si中元素的关联系数rij可由下式确定：

　　

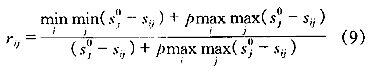
　　式中 rij——与S0在第j个因素处的关联系数
　　　　　P——分辨率系数，在0～1之间取值，一般取0.5
　　由式(9)计算可得关联系数，以矩阵形式表示为：

　　

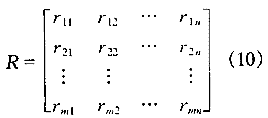
1.6 关联度的计算
　　关联度是作为衡量指标序列相似程度的测度，为［0，1］区间内变化的量，且关联度越接近1，序列与理想方案的相似程度越大；反之，关联度越接近0，序列的相似程度越小。各待选方案与理想方案的关联度μi的计算可由下式得到：

　　

1.7 结果分析
　　对关联度μi进行从大到小排序，选择关联度最大的方案作为优选方案。并对关联度的排序结果和优选方案作进一步分析说明。

2 模型的应用

　　钱塘江流域某城市污水处理厂的设计规模为5×10⁴m³/d，工程方案拟在三沟式氧化沟、SBR法、A²/O法和AB法4种工艺中选择，分别以A1、A2、A3和A4来表示这4种工艺。选择的评价指标有工艺技术成熟度、费用现值(主要为主体构筑物 和污泥处理部分的基建投资和运行电费现值之和)、占地面积、操作管理、出水稳定性和除磷脱氮效果6项，分别以a1、a2、a3、a4、a5、a6 来表示。除费用现值和占地面积根据概算得到外，其余4项模糊指标经多位专家打分后取平均值得到。
　　最后得到4种工艺方案和理想方案A0的评价指标值，如表1所示。

表1 4种工艺方案和理想方案的评价指标值 方案 a₁(%) a₂(万元) a₃(hm²) a₄(%) a5(%) a6(%) A1 90 6505.1 1.48 85 80 75 A2 80 3938.4 0.55 80 85 80 A3 80 5892.7 0.92 65 75 90 A4 85 4762.1 0.78 65 80 65 A0 100 3600.0 0.53 100 100 100

2.1 评价指标矩阵的建立和规范化
　　由表1中的数据可得4种工艺方案和理想方案的评价判断矩阵：

　　

　　采用式(3)、(4)对矩阵A进行规范化得到规范化矩阵：

　　

2.2 评价指标权重的确定
　　由专家对城市污水处理厂工程方案的6项评价指标进行两两比较，由比较结果得到指标权重的判断矩阵：

　　

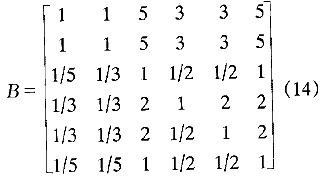
　　应用式(7)、(8)，得到6项评价指标的权重为：

　　w=［0.326 9　　0.326 9　　0.063 9　　0.116 5 　0.101 9　　0.063 9］　　(15)

2.3 关联度系数的确定
　　对式(13)进行s0j-sij的操作，得到：

　　

　　由式(16)可得：
　　

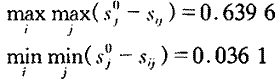
　　将此结果和分辨率系数p=0.5代入式(9)，得关联系数

　　

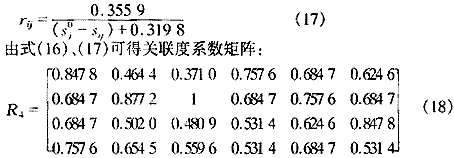
2.4 方案优化结果及分析
　　根据式(18)、(11)得到4种工艺方案的综合关联度(见表2)。

表2 4种工艺方案的综合关联度 工艺 三沟式氧化沟 SBR法 A²/O法 AB法 综合关联度μ 0.6506 0.7752 0.5984 0.663 0

　　由表2可知，综合关联度μ2＞μ4＞μ1＞μ3，即4种工艺方案的优先顺序为：SBR法→AB法→三沟式氧化沟→A2/O法。因此，对该城市污水处理厂工程 来说，SBR法为最优方案，AB法为次优方案。
　　从6项评价指标的权重wi可以看出，对于钱塘江流域来说，工艺成熟度和总费用的权重最大，而占地面积和除磷脱氮的权重最小。由于SBR工艺方案的总费用要比其他3种工艺小得多，出水稳定性又最高，在工艺成熟度相差不大的情况下，因评价指标权重的影响，使得SBR工艺方案的综合关联度μ值要远大于其他3种工艺方案。
　　AB法比三沟式氧化沟的总费用和占地面积要小得多，工艺成熟度二者相近，操作管理和除磷脱氮效果AB法偏差，但在评价指标权重的影响下，AB法方案的综合 关联度μ值要略高于三沟式氧化沟。

3 结论

　　 ① 模型中引入了模糊数学的灰色关联分析法和工程优化中多目标决策思想，并对各评价指标应用了权重的概念，其与现行的城市污水处理厂可行性分析中以经济数据为主的方案选择相比，更能客观地反映系统要素的全面影响，使评价结果更为科学合理，为污染源控制方案 的优化选择提供了较好的科学依据。
　　② 一般方案的评价指标有定量和定性两种指标，灰色关联的多目标决策模型就是通过把定性指标量化，并与定量指标相结合，应用特定的数学方法得到混合型的量化标度——综合关联度μ，由μ值的大小来评判方案的优劣，因而具有一定的科学性与实用价值。
　　③ 该模型应用于钱塘江流域某城市污水处理厂的工艺方案优化选择中，工艺技术和总费用指标的权重最大，操作管理和出水稳定性次之，占地面积和除磷脱氮的权重最小；优化选择 结果是SBR法为最优方案，AB法为次优方案。

参考文献：

　　［1］ 欧雷S S.工程优化原理及应用［M］.祁载康等译.北京：北京理工大学出版社，1990.
　　［2］ 贺仲雄，赵大勇，等.模糊数学及其派生决策方法［M］.北京：中国铁道出版社，1992.
　　［3］ 向跃霖.环境治理工程方案的灰色优选新模型及其应用［J］.环境工程，1998，16(3)：52-55.
　　［4］ 张建锋，黄廷林.关中地区污水处理工艺选择的系统分析［J］.环境工程，1999，17(3)：61 -64.
　　［5］ 吴育华，郑道英，等.海口长流污水厂工艺方案多目标评价与选择［J］.中国给水排水，1999，15(4)：41-43.

---

　　电　　话：(0571)87961285×8503
　　传　　真：(0571)87051838
　　收稿日期：2001-09-10