组合推流反应器模型用于河道需氧量计算

孙从军，张明旭
(上海市环境科学研究院， 上海 200233)

　　摘　要：建立了简便的组合推流反应器模型，它可用于上海苏州河的曝气需氧量计算和充氧后的水质预测。利用该模型可计算出在调水情况下，为确保各河段的溶解氧达到2mg/L的预期目标，苏州河的北新泾—河口段水体的总需氧量为24.72tO₂/d。
　　关键词：河道曝气；组合推流反应器；需氧量；计算方法
　　中图分类号：X505
　　文献标识码：A
　　文章编号：1000-4602(2002)09-0016-04

Use of combined Plug-flow Reactor Model for Calculating Oxygen Demand of River Reach
SUN Cong-jun, ZHANG Ming-xu
(Shanghai Academy of Environmental Science,Shanghai 200233,China)

　　Abstract：A simple model—combined plug-flow reactor model was set up to calculate the
aeration requirement in Suzhou Creek and predict the water quality after aeration.Based on the calculation made by the model,total oxygen demand for the secti on from Beixinjing to estuary is calculated to be 24.72 to?2/d under flow regulation condition,so as to ensure that all river sections may reach expected targe t,i.e.,DO=2mg/L.
　　Keywords:aeration; integrated plug-flow reactor; oxygen demand; calculation method

1 组合推流反应器模型

　　该模型是根据推流反应器的作用原理，在充分利用苏州河现有水质、水力资料的基础上，对相关边界条件做了合理的简化和假设并综合考虑了多种耗氧和复氧作用而建立起来的。?
1.1 计算原理及假设
　　将苏州河的河道曝气复氧工程近似看成多个推流式反应器^[1]的串联组合，其计算原理用图1表示。

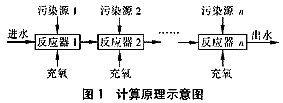
　　为简化计算而作如下假设：
　　① 各污染源只是在各反应器首端集中进入；
　　② 入流污染源的水质、水量不随时间变化；
　　③ 入流污染源与反应器进水立即混合均匀。
1.2 模型构成
1.2.1 水力计算公式
　　模型中任意一个(第n个，n≥2)反应器的水力计算公式如下：
?　　　　Qn=Q_n-1+Q_p-n?　　　　　　?(1)
?　　　　un=Qn／（Sn′×86400）　　　(2)
?　　　　tn=Ln／（un×86400）　　　　(3)?
　　式中 ?Qn——第n个反应器的流量，m³/d
?　　　　Q_n-1——第n-1个反应器的流量，m³/d
?　　　　Q_p-n——第n个污染源的流量，m³/d
?　　　　un——第n个反应器的平均流速，m/s
?　　　　Sn′——第n个反应器的过水断面积，m²
?　　　　tn——第n个反应器的水力停留时间，d
?　　　　Ln——第n个反应器的长度，m
1.2.2 耗氧和复氧因子计算公式
　　模型中任意一个(第n个，n≥2)反应器的耗、复氧因子计算公式如下：
?　　C_0-n=C′_0-n-k₀t_n　　　　　　(4)
?　　C1-n=C′_1-nexp(-kctn)?　　(5)
?　　C_2-n=C′2-nexp(-kNtn)?　　(6)
?　　C_3-n=(C_s-n-C_0-n)[1-exp(-kLatn)]?(7)
?　　O_s-n=Snαn?　　(8)
?　　Oa-n=Snβn?　　(9)?
　　式中 ?C_0-n——第n个反应器出口的还原物质浓度，mg/L
?　　　　 C′_0-n——第n个反应器进口的还原物质浓度，mg/L
?　　　　 k₀——无机还原物质的耗氧速率，mg/(L·d)
?　　　　　kc——生化反应速率常数，d^-1
?　　　　　C_1-n——第n个反应器出口的BOD₅浓度，mg/L
?　　　　　kN——硝化反应速率常数，d^-1?
?　　　　　C_2-n——第n个反应器出口的氨氮浓度，mg/L
?　　　　　C_3-n——大气复氧量，mg/L
?　　　　　C_0-n——第n个反应器水体的溶解氧浓度，mg/L
?　　　　　C_s-n——第n个反应器在计算水温下的饱和溶解氧，mg/L
?　　　　　C′_1-n——第n个反应器进口的BOD₅浓度，mg/L， 可用下式计算：
?　　　　　C′_1-n=[Q_n-1C_1-(n-1)+Qp-nCp-C-n]／Qn　　　　　(10)?
　　式中
?　　　　C_1-(n-1)——第n-1个反应器出口的BOD₅浓度，mg/L
?　　　　C_p-C-n——第n个污染源的BOD₅浓度，mg/L
?　　　　C′_2-n——第n个反应器进口的氨氮浓度，mg/L，可用下式计算：
?　　　　C′_2-n?=Qn-1C′2-(n-1)+Qp-nCp-N-nQn　　　　(11)?
?　　　　C_2-(n-1)——第n-1个反应器出口的氨氮浓度，mg/L
?　　　　C_p-N-n——第n个污染源的氨氮浓度，mg/L
?　　　　kLa——复氧系数，d-1，可用O′Connor—Dobbins公式^[2]计算：
?　　　　KLa=（128(DMun)0.5）／h_n^1.5?　　　12)?
　　式中　hn——第n个反应器的平均水深，m
?　　　　D——氧在水体中的扩散系数，m²/d，当水温为20℃时，DM(20)=2.036×10^-9m²/d。各种水温下的DM值可用下式计算：
?　　　　D?M=1.76×10^-4×1.037T-20　　　(13)?
　　式中　T——设计水温，℃
?　　　　Os-n——第n个反应器的底泥耗氧量，kg/d，可用下式计算：
?　　　　Os-n=Snαn/1000　　　(14)?
　　式中?Sn——第n个反应器的底面积，m²
?　　　　αn——第n个反应器的底泥耗氧强度，g/(m²·d)
?　　　　Oa-n——第n个反应器的藻类复氧量，kg/d，可用下式计算：
?　　　　Oa-n=Snβn／10000　　　(15)?
　　式中?βn——第n个反应器的藻类复氧强度，kg/(hm²·d)
1.2.3 需氧量计算公式 ?
　　模型中任意一个(第n个)反应器的需氧量可用下式计算：
?　　　　On=[Qn(C′0-n-k0tn)／1000+[1.4QnC′1-n(1-exp(-kctn))／1000]+[4.7QnC′2-n(1-exp(-kNtn))／1000+Os-n]-[Qn-1C0-(n-1)／1000]+Oa-n+[Qn-1C3-n／1000]　　　　　　　(16)?
　　式中 ?On——第n个反应器的需氧量，kg/d
?　　　　 C0-(n-1)——第n-1个反应器出口的溶解氧浓度，mg/L
　　组合推流反应器模型近似于一维稳态水质模型，两者的不同之处在于一维稳态模型的溶解氧计算中考虑了各耗氧、复氧因子对水体溶解氧的瞬时影响，在时间坐标或沿河流方向上是连续的。此种方法的溶解氧浓度或需氧量计算是反应器中各项耗、复氧量的简单代数和，是一种近似的计算方法，而将河段分成多个反应器是提高其计算精度的主要手段。
　　另外，组合推流反应器模型未考虑黄浦江潮汐对苏州河最下游河段水质的稀释作用，计算结果比较接近于落潮和采用闸门调控时(单向流时)的实际水质。

2 模型的应用

　　1999年7月28日—8月28日，有关部门采用控制苏州河沿线的干、支流闸门启闭的方式成功地进行了苏州河调水试验，同时得到了有关苏州河及其支流的水质、水量和其他污染源的大量监测数据和资料。计算中使用的基础数据是在此次调水相对稳定期(8月17日—8月21日)内取得的数据(取5d平均值)，这样便于将模型计算的结果与实测数据相比较，并在此基础上进行需氧量的计算。
2.1 计算参数
　　将苏州河位于上海市内的河道分为10个不同长度的设计河段(反应器)，其计算参数及其来源见表1。

表1 模型计算参数及其来源 项 目 取 值 来 源 设计水温(℃) 25 苏州河夏季平均水温 生化反应速率常数(d^-1) 0.25 研究结果 硝化反应速率常数(d-1) 0.08 研究结果 还原物质耗氧速率[mg/(L·d)] 4.8 研究结果 底泥耗氧强度[g/(m²·d)] 1(黄渡以上河段)；2(黄渡—纪王河段)；6(华漕以下河段)。 研究结果 藻类复氧强度[kg/(hm²·d)] 40(华漕以上河段) 参考文献[ 3] 河道水深(m) 3(华漕以上河段)；3.5(华漕以下河段)。 研究结果 河宽(m) 40(武宁路桥以上河段)；45(武宁路桥—江宁路桥河段)；50(江宁路桥—新昌路桥河段)；55(新昌路桥—河口河段)。 研究结果 氧分子扩散系数(m²/d) 2.11×10^-4 由文献[2]计算而 得 注：研究结果见《苏州河河道曝气复氧工程方案研究 》(上海市环境科学研究院，1999年5月)。

2.2 计算结果
2.2.1 水质
　　在调水情况下应用组合推流反应器模型对苏州河水质进行了测算，结果见表2。同期各实测断面的水质见表3。

表2 调水情况下苏州河水质计算结果 断面名称 距离(km) COD(mg/L) BOD₅(mg/L) NH₃-N(mg/ L) DO(mg/L) 赵屯 53 21.6 5.7 1.0 1.95 白鹤 41 21.4 5.4 2.6 1.99 黄渡 33 22.4 5.6 1.3 2.08 纪王 27.5 24.8 6.0 1.6 2.12 华漕 22 24.3 7.0 2.1 1.83 北新泾 17 29.8 10.6 4.5 0.31 冕宁路 13.8 29.8 10.4 4.6 0.00 武宁路桥 10.3 29.5 10.0 4.6 0.00 江宁路桥 7.6 29.0 9.7 4.6 0.00 长寿路桥 5.2 28.6 9.4 4.6 0.00 新昌路桥 3.2 28.4 9.1 4.6 0.00 河口 0 28.0 8.7 4.6 0.00

表3 苏州河各监测断面的实测水质 断面名称 距离(km) DO(mg/L) COD(mg/L) BOD₅(mg/L ) NH₃-N(mg/L) 赵屯 53 1.95 21.6 5.7 0.95 黄渡 33 2.07 22.4 5.6 1.3 华漕 22 1.92 26.7 7.6 2.05 北新泾 17 0.34 32.8 8.6 4.15 冕宁路 13.8 0.16 35.3 9.7 4.16 武宁路桥 10.3 0.23 31.6 8.2 4.77 新昌路桥 3.2 0.37 34.7 9.1 4.45 河口 0 0.53 27.6 6.5 2.65 注：表中数据见《苏州河第三次调水试验第二阶段总结报告》(苏州河第三次调水试验技术小组 ，1999年9月)。

　　由表2、3可以看出，除由于模型未考虑黄浦江水对苏州河最下游河段的稀释作用而使计算得到的河口处的水质 均较实测数据高外，其他计算结果与实测数据之间均呈较好的相关性(尤其是在华漕和北新泾这两个断面，模型计算结果能较准确地反映这两处水体的实际水质状况)，这意味着利用该模型计算得到的结果能够较好地反映实际状态下苏州河水质的变化情况，在此基础上计算 得到的需氧量能够较好地满足苏州河水体的耗氧需求。
2.2.2 需氧量
　　由表3可知，在调水情况下北新泾断面下游至河口一段溶解氧仍然偏低(DO＜0.5mg/L)，故为彻底消除苏州河的黑臭状态，必须适当提高苏州河水体的溶解氧水平。这里将苏州河曝气复氧工程的近期目标设定为DO≥2mg/L，即满足《地面水环境质量标准》(GB3838—88)中的V类水体标准。而同在调水情况下，应用组合推流反应器模型对苏州河(北新泾—河口)曝气复氧工程的需氧量进行计算，结果见表4。

表4 调水情况下需氧量计算结果 断面名称 距离(km) COD(mg/L) BOD₅(mg/L) NH₃-N(mg/ L) DO(mg/L) 需氧量(kg/d) 赵屯 53 21.6 5.7 1.0 1.95 0 白鹤 41 21.4 5.4 2.6 1.99 0 黄渡 33 22.4 5.6 1.3 2.08 0 纪王 27.5 24.8 6.0 1.6 2.12 0 华漕 22 24.3 7.0 2.1 1.83 4060 北新泾 17 29.6 10.6 4.5 2.00 5720 冕宁路 13.8 27.9 10.0 4.5 2.00 4280 武宁路桥 10.3 26.3 9.3 4.4 2.00 3240 江宁路桥 7.6 24.8 8.6 4.4 2.00 3150 长寿路桥 5.2 23.6 8.1 4.3 2.00 2570 新昌路桥 3.2 22.6 7.6 4.3 2.00 1700 河口 0 21.8 6.9 4.2 2.00 0 合计 　 　 　 　 　 24270

　　由表4可知，在调水情况下为确保苏州河各河段的DO达到2mg/L的预期目标，苏州河北新泾—河口段水体的总需氧量为24.72 tO₂/d，充氧后苏州河的水质可得到一定程度的改善。
　　需要指出的是，在苏州河水体中维持一定浓度的溶解氧的意义不仅在于能够消除黑臭和去除COD负荷，而且能使苏州河水体具有一定的抗冲击污染负荷(暴雨径流、泵站排水、污染事故等)能力，对于水体生态系统的重建和恢复具有非常重要的意义。

3 结论

　　将组合式推流反应器模型用于苏州河的曝气复氧工程的水质预测及需氧量计算，通过计算得到在调水情况下为确保达到各河段的溶解氧≥2mg/L的预期目标，苏州河的北新泾—河口段水体的总需氧量为24.72tO₂/d。

参考文献：
　　[1]秦麟源.废水生物处理[M].上海：同济大学出版社，1989.
　　[2]顾夏声.废水生物处理数学模式[M].北京：清华大学出版社，1993.
　　[3]傅国伟.河流水质数学模型及其模拟计算[M].北京：中国环境科学出版社，1987.

---

　　作者简介： 孙从军(1972-)，男，安徽蚌埠人，上海市环境科学研究院水环境研究所工程师，硕士，主要从事水环境污染控制方面的科研、设计工作。
　　电　话：(021)64085119×2320 13501796369
　　E-mail:suncj@sina.com.cn
　　收稿日期：2002-03-05