理想凝聚沉淀试验数据的整理与分析

周毅1，余蔚卿2，张永波3
（1． 武汉大学土建学院市政工程系，湖北 武汉430072；2．长江水利委员会，湖北 武汉430010；3．广东省环境检测中心，广东 广州 510045）

　　摘　要：在凝聚性沉淀试验的数据整理中，要找出去除率c、表面负荷μ0和停留时间t之间的关系，通常用人工计算和手工画曲线的方法。如果利用Matlab编程整理数据，可以最大限度地减小人为因素的影响，并充分利用已有的数据，快速、高效、准确地得出计算结果，并可以对结果进行直观地调整、分析判断，从而优化设计参数。
　　关键词：凝聚；沉淀；混凝计算；表面负荷；停留时间
　　中图分类号：TP391
　　文献标识码：A
　　文章编号：1009－2455（2003）02－0012－03

Sorting out and Analyses of ideal Coagulation Sedimentation Experimental Data
ZHOU Yi，YU Wei-qing，ZHANG Yong-bo

　　Abstract：In sorting out the experimental data of coagulating sedimentatation，manual calculation and curving are usually used to find out the relationship among the removal rate C，the surface load μ0 and the residence time t.If Matlab program is used for the sorting out of the data，artificial effects can be minimized，full use can be made of the data already available to get the results of calculations quickly，efficiently and accurately，and the results can be adjusted．analyzed and evaluated directly，which will optimize the design data．
　Keywords：coagulation；sedimentation； coagulation calculation；surface load：residence time

　　对凝聚性沉淀试验数据的整理是设计沉淀池的一个重要步骤。试验首先要测出不同深度、不同沉淀时间下悬浮物的去除率，然后采用插值法绘出"去除率等值线"，选定某一深度，计算出不同停留时间下得到的总的去除率，最后将结果点绘成停留时间 t与去除率 C的关系曲线。本文对matlab编程整理凝聚性沉淀试验数据进行了研究。

1 理想凝聚沉淀的数学模型

　　从实验数据可以看出：悬浮物去除率C是沉淀深度ho、停留时间L的函数，记作C=f（h0，t）。同时，可以根据公式(1)计算截流沉速。
　　μ0＝ho／t 　　　　　　(1)
　　式中：
　　　　μ0--理想沉淀池的截流沉速；
　　　　ho--沉淀深度；
　　　　t--颗粒在沉淀区中的停留时间。
　　由于表面负荷在数值上等于截流沉速，所以又可以换算出表面负荷与去除率的函数关系，点绘出二者的关系曲线。因此，C又可以看作μ0和t的函数C=g（μ0，t）。当μ0，t，ho中的任意两个参数确定后，C的值也随之确定。根据C与t，ho的测定结果，利用数值插值的有关计算方法进行三次插值，可以得到任意时间、任意深度的去除率计算结果。并且结果可用三维或二维坐标图表示出来。

2 数据处理

2．1 Matlab方法
　　Matlab是集数学计算、图形处理和程序语言设计于一体的著名数学软件。与其它高级语言相比，Matlab提供了一个人机交互的数学系统环境，并以矩阵作为基本的数据结构，可以大大节省编程时间。
2．2 对凝聚沉淀的分析
　　为了分析问题的方便，把最初的凝聚性悬浮物浓度当作100％，以后所测得的去除结果都用相对去除率表示。
2．2．1 计算某浓度下的去除率
　　假定池深为ho，选定不同的停留时间，计算出某一时刻水中悬浮物去除浓度。总的去除百分率为：
　　　　　　C=(1-C0)＋∫₀^co（Ui／μ0）d Ci （2）
式中：
　　C0--所有沉速小于μ0的颗粒重量占原水中全部颗粒重量的百分率；
　　μ0--理想沉淀池的截流沉速；
　　μi--小于截流沉速的颗粒沉速；
　　Ci--所有沉速小于U；的颗粒重量占原水中全部颗粒重量的百分率；
　　dCi--具有沉速为认的颗粒重量占原水中全部颗粒重量的百分率。
　　对于上式中积分的处理，可以近似地认为：

式中：
　　h0--沉淀池深度；
　　hi--去除率等值线图中相邻两条等值线的中点所对应的深度；
　　δCi--去除率等值线图中相邻两条等值线所代表的去除率之差。
　　δCi取值越小划分得越密，积分与累积求和的差值越小，精度就越高。利用Matlab编程可以很方便地实现这一点。
　　已知池深为h0，需要画出0~t时段上的总去除率曲线，方法如下：
　　①根据前述插值拟合的结果，可以找出在不同时刻、在h0深度处沉速大于或等于μ0的已全部去除的颗粒的去除率CO。
　　②对于某一时刻t，根据插值拟合的结果，找出不同深度处的去除率，代人（3）式，可以求出在h0深处，未能全部去除悬浮物的去除率。
　　③总去除率由以上两部分相加即可求得。
　　假定不同的沉淀深度，重复上述①~③步，可得出不同深度、不同时间下的总的去除率。
这一计算结果与根据实验结果得出的二维值拟合结果不会相同。前述插值计算的结果反映的是某一时刻、某一深度该点的去除率。而后者是考虑了沉淀池的出水实际上是某时刻不同深度处的出水相混合的结果。假定不同的沉淀深度，会有不同的总的去除率。或者说，将不同深度的去除率作了平均化计算，取其平均数。
3 计算实例
　　例：凝聚性悬浮物的质量浓度为400mg／L。静置沉淀试验所得的沉淀时间和取样深度以及相应的悬浮物去除率如表1；

表1悬浮物去除率

取样深度／m 不同沉淀时间（min）的去除率/% 5 10 20 40 60 90 120 0.61 41 50 60 67 72 73 76 1.22 19 33 45 58 62 70 74 1.83 15 31 38 54 59 63 71

　　根据上表的试验数据，试确定采用平流沉淀池的悬浮物去除率、表面负荷和停留时间之间的关系。
此时的初始条件为：t＝0时，任意深度处的去除率 C＝0；h＝0（而t≠0）时，去除率C＝100％，插值的结果用三维图形表示如图1所示。

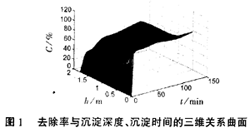
　　从图1可以看出，池深越浅、沉淀时间越长，去除率越高。
　　例如h0＝1．83m时，计算结果如图2。

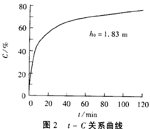
　　由图2可以看出：当沉淀时间在0~40min以内时，去除率随时间增长很快；超出该范围时，去除率随时间增长缓慢。因此将时间控制在40min左右时，既经济又高效。超出该范围延长时间，对去除率的影响不大。
　　由于μ0=h0/t＝1.83／t，所以利用Matlab进行简单地换算即可计算出表面负荷μ0与去除率C之间的关系，绘出关系曲线，如图3所示。

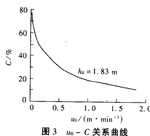
　　至此我们得出了在池深为1.83m时，在不同停留时间或不同表面负荷时所对应的去除率。
　　图3O－c关系曲线
　　如果改变有效池深，可以得出另外一条t-C曲线和μ0一C曲线。例如，池深h0＝1．5m时，t一c曲线和μ0一c曲线如图4、图5。

　　

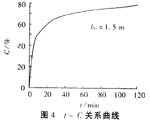
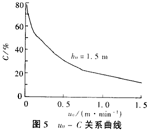
　　比较图2和图4，可以发现：相同停留时间，池深浅时，去除率高，并可以在曲线图上准确地找出某一深度时t-C的准确对应关系。
3．1 计算结果的验证
　　假定有效池深1.83m，停留时间35min，则相应的表面负荷为：μ0＝75.3m3／（m3·d）。利用Matlab计算出的总去除百分数为64.4％，手工计算的总去除百分数为60.9％。
　　如果假定池深和停留时间不同，还可以计算出不同的去除率。
　　利用Matlab计算与手工计算有一定的出入，其主要原因分析如下：
　　①计算机计算的去除率略高于手算的去除率，主要是由于在水深浅时，计算机的程序中对深度作了较为精细的划分。且在理想条件下认为h0＝0时，C＝100％。而手算时，并没有将这些因素全部考虑进去。
　　②原始数据中所取的相邻深度相差较大，而利用Matlab计算是为了有较高的精度，深度划分、时间划分都较细，而手算很难做到这一点，因此二者结果有一定差别。但是，其计算思路、方法是一样的，本质上是一致的。

4 结论

　　利用Matlab整理理想凝聚沉淀试验数据，不仅减小手算工作量，提高了计算精度，而且结果可视化效果很好，能直观地反映出变化。根据不同试验数据，可以利用相同的计算程序，计算出不同水质在怎样的停留时间和沉淀深度下去除效果最有效，即达到最优化设计。

---

　　作者简介：周毅（1975－），男，湖北黄冈人，讲师，硕士，主要从事水处理及给排水系统优化设计的研究和教学工作，电话（027）67803833，yzhou99＠sohu.com.