应用计算流体力学(CFD)方法优化给水厂清水池设计的原理和中试研究
| 论文类型 | 技术与工程 | 发表日期 | 2004-12-01 |
| 来源 | 环境科学与工程 | ||
| 作者 | 刘文君,崔磊 | ||
| 摘要 | 刘文君*,崔磊 (清华大学环境科学与工程系,北京,100084) 摘要: 本文介绍了应用计算流体力学(Computational Fluid Dynamics,CFD)优化给水厂清水池设计的原理和应用方法,并以863示范工程为物理模型,通过建立中试装置的CFD模型,得到清水池数学模型的液龄分布函数和累计液龄分布函数。研究 ... | ||
刘文君*,崔磊
(清华大学环境科学与工程系,北京,100084)
摘要: 本文介绍了应用计算流体力学(Computational Fluid Dynamics,CFD)优化给水厂清水池设计的原理和应用方法,并以863示范工程为物理模型,通过建立中试装置的CFD模型,得到清水池数学模型的液龄分布函数和累计液龄分布函数。研究比较了CFD计算和实际中试模型示踪试验的结果,表明二者的误差在可接受的范围之内,因此证明应用CFD方法优化清水池设计是可行的。
关键词:CFD模型;清水池;水力效率;停留时间
The Principles and Pilot Tests of Applying Computational Fluid Dynamics (CFD) Method in Optimizing the Design of Clearwell
LIU Wen-jun﹡, CUI Lei
Abstract: This paper introduces the principles and application procedures of the Computational Fluid Dynamics (CFD) method in optimizing the design of clearwell. In this study, a CFD modeling of the pilot-scale clearwell prototyped an 863 demo-project was established, which described the detailed information of the local characteristic of the flow domain which could not be visualized in trace tests. The residence time distribution (RTD) curves and cumulative residence time distribution (CRTD) curves of the pilot-scale clearwell were obtained, which was compared with those from the pilot-scale trace-tests. The errors between the results from CFD calculation and trace-tests were within the acceptable range, which demonstrated that CFD method can be used in optimizing the clearwell design.
Key words:CFD model; clearwell; hydraulic efficiency; residence time
目前国内已开始研究改善清水池的流体力学特性以提高消毒效果和控制消毒副产物的产生[1,2]。CFD(Computational Fluid Dynamics)就是利用计算机求解流体流动的各种守恒偏微分方程组的技术,其中涉及流体力学尤其是湍流力学、计算方法以及计算机图形处理等技术。流体的流动可用Navier-Stokes方程描述,因此CFD中最基本的数学物理模型即为粘性流体的Navier-Stokes方程。
目前在清水池流体力学特性研究中普遍通过示踪剂试验求得停留时间函数模型(RTD)来表达清水池的水力效率[1-3]。但通过示踪试验测定清水池时间分布函数费时费力,而且有时可能不能实现。随着电脑运行能力和计算流体力学方法的不断进步,对流场和传质的高精度数值模拟已成为可能。通过CFD模拟计算可以很容易、精确且直观地得出清水池内水流流态和速度分布,揭示出很多物理模型无法表达的信息,如局部流速、短路流形态、单个颗粒停留时间和运行轨迹等,优化清水池设计。本研究以国家863示范工程深圳水务集团笔架山水厂#2清水池为模拟对象,采用CFD方法计算清水池在不同结构配置条件下的水力学特征,并与中试模型试验结果进行比较,在证明CFD方法可行的前提下,用CFD方法优化给水厂清水池设计。本文主要介绍CFD方法原理和CFD计算结果与中试结果的比较,CFD方法的应用结果将另文介绍。
1 数学模型的建立和求解
1.1 数学模型的整体框架
建立模型的步骤分为数学描述、数值求解、边界和初始条件设置三部份。数学模型建立后便是数学模型的解析,包括迭代求解、数据采集与后处理、检验模拟准确度三部分,流程图如图1。
图1概括了建立数学模型的基本过程,整个过程分为建立数学模型和解析数学模型两部分,而建立数学模型又分为几何模型和物理模型两方面,其中物理模型又包括连续相流体和分散相颗粒两个子模型。
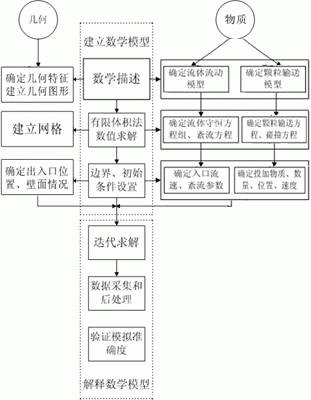
图1 数学模型整体框架
Fig.1 Mathematical model frameworks
1.2 两相流数学模型基本概念
1.2.1 连续相(水相)紊流模型
由于一般流体处于紊流状态,因此本模型采用紊流RNG k-ε 模型。它最重要的两个方程就是关于两个最重要参数-动能k和能量耗散ε的方程。
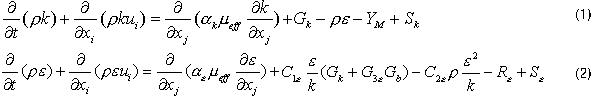
其中Gk是由层流速度梯度而产生的湍流动能,Gb是由浮力而产生的湍流动能,YM是由于在可压缩湍流中过渡的扩散产生的波动,C1,C2,C3是常量,αk和αε是k方程和ε方程的湍流Prandtl数,Sk和Se由用户定义[5]。
1.2.2分散相(示踪剂)水力输送模型
本文对颗粒相采用欧拉-拉格朗日分散相模型,对颗粒的运行轨迹和停留时间进行模拟,其最重要的方程是颗粒在流场中的受力方程[4]:
![]() (3)
(3)
其中u为连续相流速,up为颗粒相流速,ρ和ρp分别为流体和颗粒密度。Fd(u-up)表示了单位质量颗粒所受的曳力。Gx(ρp-ρ)/ρp表示单位质量颗粒所受的重力。Fx为颗粒受到的其他力。
1.3 数学模型涉及的相关公式
CFD软件根据以Navier-Stokes方程为基础的流体流动和能量平衡关系进行计算求解,使用者可以根据自己的模型选择特定的平衡关系包含到自己的模型中。实际上,根据模型合理选择特定的平衡关系是一种合理的简化。
Fluent软件中,这些平衡关系来源于Navier- Stokes方程中关于质量、能量和动量的守恒,还有如热量传递、物质混合或反应、k-ε紊流模型等[4]。
1.3.1 质量守恒方程
对于多组分系统,质量守恒方程描述如下:
![]() (4)
(4)
其中mi为系统中各组分的局部质量分数,Ji‘,i为组分i‘由于浓度梯度引起的扩散通量,Ri‘为由于化学反应而产生或损耗的质量速率,Si‘为其他源项的质量速率。
1.3.2 动量守恒方程
在惯性(非加速)坐标系中i方向上的动量守恒方程为:
![]() (5)
(5)
其中p是静压,τij是应力张量,ρgi和Fi分别为i方向上的重力体积力和外部体积力(如离散相相互作用产生的升力)。Fi包含了其他的模型相关源项,如多孔介质和自定义源项。
1.4 建立网格
如上所述,描述流场的一系列偏微分方程通过有限体积方法将流场划分为众多小区域后,再由求解器进行计算求解[5]。
网格的密度和质量可以由用户自己决定,并且影响最终的求解过程。过于粗糙的网格,往往只给出流场一些简单的轮廓,而无法给出详细且精确的结果,甚至无法揭示出流场的本质特征。
当设置好模型几何图形的边界条件后,就可以用上面提到的平衡方程和边界条件对所有网格进行迭代计算,从而得到特定问题的收敛解。
1.5 网格精度
由于网格决定着模型的准确度,所以生成合理的网格是建立数学模型的一个关键步骤。生成网格不但要考虑其细密程度来提高模拟过程的细节准确程度,又要避免由于网格过于复杂带来的漫长计算时间。一般来说,需要找到一个最优化的网格密度来满足模型的计算精度和计算时间,再提高精度也不会更多地反映出需要的流场细节,而减少精度又会掩盖住流场的本质特征。
1.6 网格结构
基于有限体积方法,对于那些流场特性变化不明显的区域,网格精度可以予以降低,而对于变化显著的地方如边界层、拐角处等地方,网格需要提高精度,减小有限体积,从而提高反映该区域流场特性变化的详细信息的准确性。图2为基于示范工程#2清水池的实际物理中试模型建立的几何模型网格图。
1.7 物理原型
CFD模拟的中试清水池几何尺寸和水力特性如表2。

图2 七挡板清水池数学模型网格图
Fig.2 Nets of the mathematical model of seven-baffle clearwell
从图2中可以看出边界层和拐角处的网格设置较细密。表1给出该网格的基本几何信息。
表1 七挡板清水池数学模型网格几何信息
Table 1 Geometrical parameters of the mathematical model of seven-baffle clearwell
表2 物理模型几何尺寸和水力特性
Table 2 Geometrical and hydraulic parameters of the pilot tests
无论对于物理模型还是数学模型,确定流场的T10/T值[1]和RTD曲线都需要进行示踪试验。示踪试验方法见文献[2]。
1.8 设置边界和初始条件
对于数值模拟的求解过程,正确设置边界和初始条件是使模拟得到收敛,特别是得到稳态解的重要保障。
1.8.1 进水口流速
确定进口处的流速则需要根据质量守恒的原则,即单位时间内三维物理模型进入流场的质量/体积等于单位时间二维数学模型进入流场的质量/体积,则有以下公式:
![]() (6)
(6)
其中,U为平均流速;
H为二维入水槽高度;
D为二维入水槽宽度。
物理模型入口管径为0.05m,流量为1.6m3/h,水面高度0.37m。
可以算得二维模型的入口处进水平均流速为
![]()
1.8.2 确定紊流模型参数
入口处紊流动能k定义为:
k=aU2
单位质量的能量耗散率ε定义为:
![]() 或 ε=1.5k1.5/ΓH
或 ε=1.5k1.5/ΓH
其中ρ为流体密度,μ为流体粘度,Cμ为一常数0.09,Rμ为紊流和流体粘度之比,ГH为水力半径。
流场边界设置见表3。
表3 数学模型边界条件设置
Table 3 Boundary conditions of the mathematical model
1.9 求解过程
计算过程可以不将颗粒相对于流体(连续相)的影响考虑在内,也可以考虑颗粒对流体的作用效果。这两种算法分别称为非耦合计算和耦合计算。由于考虑到颗粒相浓度很小,和连续相相比,颗粒对流体的作用可以忽略,所以本文的模型采取两相非耦合模型进行计算。
1.10 数据采集和后处理
模型的两相经过求解计算后,可以得到每个控制体积内两相的各项属性,包括流体的流速、压强、颗粒的流速以及颗粒的轨迹和在流场中的停留时间。这里,对物理原型的采样方法适当简化,即以相同的时间步长对颗粒出口情况进行统计,来得到其时间停留密度曲线和累计液龄分布函数曲线。T10则由F( t )上最接近F( t )=0.1的两个点线性插值求得。
2 模拟结果和准确度验证
2.1 流场的模拟
模拟的流场速度等值线图见图3。
如图3所示,通过流场出入口的流体流速变化明显。流场内部,特别是挡板间的长流道部分,流体均匀流特性较好,拐角部分流速变慢,越远离挡板,速度越小。挡板的设置可以增强流体的均匀性,但同时也会造成短路流,拐角部分矢量图的局部放大图如图4。

图3 数学模型速度等值线图
Fig.3 Velocity field of mathematical model

图4 数学模型(基准)拐角部分矢量图
Fig.4 Vector field of the mathematical model in turning area
从图中可以看出,在靠近外墙的部分,造成了很多与流体速度逆向的短路流。短路流的存在会影响示踪剂在流场内的停留时间,进入短路流的颗粒需要很长时间才能摆脱,重新回到主流体的行进过程当中。
2.2 示踪剂的模拟
对于单个粒子来说,进入流场后,随着流体流动,直至从出口出逃逸。典型单个粒子在流场中受到短路流影响的轨迹见图5。
颗粒进入挡板拐角处外侧和拐角后流体内侧速度很小的短路流后,增加了其停留时间,可见由于挡板设置造成的短路流对于流场的水力运输效率产生了负面的影响。表4给出了物理模型和数学模型的一些水力效率评价参数比较。图6、图7为CFD模拟计算结果与中试示踪试验结果比较。可以看出,CFD模拟计算结果与试验实际测出的液龄分布函数和累接液龄分布函数基本一致。结果可以接受,但二者得出的T10/T值误差为26.7%,还需进一步提高CFD的精度。

图5 数学模型(基准)单颗粒轨迹线图
Fig.5 Single particle trace of the mathematical model
表4 数学模型模拟效果比较
Table 4 The comparison of the mathematical model and pilot tests

图6 数学、物理模型累计液龄分布函数比较
Fig.6 The comparison of the cumulative residence time distribution curves from CFD calculation and pilot tests
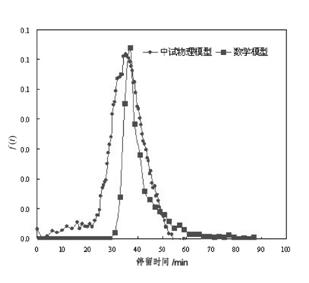
图7 数学、物理模型液龄分布函数比较
Fig.7 The comparison of the cumulative residence time distribution curves from CFD calculation and pilot tests
3 结论
本文介绍了采用计算流体力学(CFD)方法模拟计算清水池内流体特性的原理、方法和应用。通过比较中试示踪试验和CFD计算结果证明CFD模拟计算的结果精度在可接受的范围,可以应用于清水池设计的优化。
参考文献:
[1] 刘文君. 清水池改进原理与应用 给水排水,2004, 30(5): 10~12.
[2] 金俊伟,刘文君. 影响清水池t10/T值的因素试验研究 给水排水,2004, 30(12): 36~39.
[3] Gil F. Crozes, James P. Hagstrom, Mark M. Clark. Improving Clearwell Design for CT Compliance. AWWA Research Fundation and AWWA, 1997.
[4] C.N. Hass. Disinfection under Dynamic Conditions: Modification of Hom’s Model for Decay. Environ. Sci. Technol.1994, 28(6):1367~1369.
[5] Fluent Inc. Fluent 6.0 Software Documentation. 2001.
[6] Fluent Inc. Gambit 2.1.0 Software Documentation. 2001.
资助项目:国家863项目“南方地区饮用水安全保障技术(2002AA601120)”
作者简介:刘文君(1968~),男,博士,副教授,研究方向:水质科学与工程。
*通讯作者: E-mail:wjliu@tsinghua.edu.cn
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 paper@h2o-china.com ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








