生存分析法在供水管网爆管分析中的应用

生存分析法在供水管网爆管分析中的应用

何 芳¹ 吴 徐² 戴 盛² 　刘遂庆³
(1广东省佛山市供水总公司 2江苏省镇江市自来水公司 3同济大学环境科学与工程学院)

　　摘要：本文提出应用生存分析法对国内城市供水管网爆管事故进行分析，介绍了生存分析的概念以及生存分析的三种方法，阐述了采用生存分析法分析爆管的优越性，探索解决爆管问题的新思路和新方法。结合江苏某市供水管道爆管数据记录，用生存分析法中的非参数分析法对供水管道进行生存分析，绘制供水管道生存曲线和危险函数曲线，描述管道生存现状和危险程度。
　　关键词：供水管网 爆管 生存分析 模型

前言

　　我国对供水管网爆管分析研究一般以传统的描述性统计方法为主。该方法用于爆管分析主要指按管径、管材、爆管时间（年、月、日）、损坏原因而进行分类、分组、汇总统计，并通过图表形式对所收集的数据进行加工处理和显示，进而通过综合、概括和分析得出反映客观现象的规律性特征。因此，它只能估算预测某一组或某一类管道的损坏趋势，而不能对单独管道的损坏情况提供有效的信息，也不能解释众多影响因素（后面被称为解释性变量或协变量）之间复杂的相互关系。
　　在供水管网爆管分析中引入生存分析方法，可以在考虑多种爆管影响因素的条件下，对某单一管道损坏趋势或事故危险性进行预测的水平。供水管道的生存分析是以爆管的维护记录为管道生存数据样本，绘制管道生存曲线、危险曲线，并建立管道危险函数方程，对管道的生存现状进行估计预测。预测结果可以为制定有效的防治爆管措施提供依据。国外已有用生存分析法研究爆管问题的应用实例，例如挪威的S.Sagrov，加拿大的Genevieve Pelletiter等研究者，其研究的成果已应用到供水管网的运行管理中^【1】。
　　本文研究内容是该方法在国内爆管分析中应用的一次探索性尝试，以期为解决目前供水管网普遍存在的爆管问题开拓了一条新思路。

1 生存分析方法简介

　　生存分析目前广泛应用于生物医学、工业、社会科学、商业等领域，尤其以在医学、生物和保险学领域应用最频繁。随着工程上对可靠性要求的不断提高，生存分析的方法已经开始在工程中被采用。
　　生存分析就是对收集来的生存数据进行处理，生存数据包括生存时间以及其影响因素。此时，生存是一个广义的概念，是某事件某状态的持续。生存分析是研究多种影响因素与生存时间有无联系以及联系程度的大小，是一种既考虑时间又考虑结果的统计方法，并可充分利用截尾数据提供的不完全信息。生存时间是指从某起点事件开始到被观测对象出现终点事件所经历的时间。生存时间的单位可以用年，月，周，日，甚至时，分，秒等表示。
　　生存分析的方法包括2种：^【5】（1）非参数法：包括生命表法、乘积极限法（K－M法）和Log－rank检验，其中生命表法、乘积极限法用于估计生存率，Log－rank检验用于单因素预后分析；（2）参数法；参数法包括两类，即生存时间T的比例危险模型和LogT的位置－尺度模型。比例危险模型又包括Cox模型、指数模型、威布尔模型、对数正态模型、对数logistic模型等，其中以COX比例危险模型应用最为灵活，故被广泛使用。
　　COX比例危险模型是一种不考虑寿命分布类型的方法，故又被称为半参数法。该模型可以辨认与寿命时间强相关的多个协变量，并分析生存时间（或生存率）与多个危险因素之间的定量关系。其模型的基本结构为:

　　h（t,X）=ho（t）·exp（b1X1+b2X2+…+bpXp）

式中，X1,X2…,Xp为影响预后因素,h（t,x）为危险度,即时刻t的失效率；
　　　 ho（t）为当所有因素（自变量）Xk都取0时的危险度,是时刻t的基准失效率（或称本底失效率）；
　　　 bi为偏回归系数，代表该因素作用的大小（不随时间变化）。
　　　 exp（bkXk）表示第k个因素Xk所产生的作用,此项作用就是使失效率ho（t）增至ho（t）·exp（bkXk）,k=1,2,…,p。参数bk采用极大似然法进行估计。
　　　 LogT的位置－尺度模型也称加速失效时间模型（Accelerated Failure Time Models）,通常以下列模型表示:

　　Y=LnT=

　　其中，βi是未知参数；σ叫做刻度参数；Z是随机项,其分布通常叫基准分布。
　　常用的寿命基准分布函数有:Weibull型、对数正态型、对数logistic型、指数型等。参数估计采用极大似然法。

2 供水管道的生存分析

2.1 供水管道生存数据的特点
　　在供水管道的生存分析过程中，管道寿命一般是指从管道安装之日起到管道第一次发生爆管的时间，时间单位为年。供水管道的生存数据以管龄作为生存时间，管道特征参数包括管材、管径、管长、埋设时间、爆管时间、道路类型、路面交通量、压力状况等，可以作为参数回归模型中的协变量。
　　生存数据分为完全数据和截尾数据（或称为删失数据）。对供水管道而言，完全数据是指被观测管道对象从观察起点至出现终点事件（即爆管）所经历的时间。完全数据提供了管道确切的生存时间，是管道生存分析的主要依据。如果在出现终点事件之前，被观测对象的观测过程终止了，此时被观测对象提供的信息是不完全的，就称之为截尾数据。供水管网的生存数据样本经常会遇到截尾数据的处理，截尾数据又分为左截尾数据和右截尾数据。由于管网维护管理记录的不完整，从管道安装到维护数据开始记录的这段时间里无维护记录，而在开始观测之前，事故可能已经发生了，但是没有这方面的记录，这样会导致左截尾数据；当维护记录中止的时候管道没有发生任何事故，发生事故的确切时间未知，但是肯定是属于一个时间段【t，＋∞】，则导致右截尾数据，如图1所示。

2.2 供水管道爆管生存分析的优点
　　将生存分析方法引入供水管道爆管分析有如下优势：
　　(1) 分析生存分析既能考虑观测对象的观测结果，又能考虑得到该结果经历的时间；把管道是否爆管作为观测目的，将管道爆管视为管道“失效”，管道正常运行视为“生存”，可以考察管道“失效”或“生存”和时间的关系；
　　(2) 生存分析可以充分利用截尾数据所提供的不完全信息；供水管道的爆裂毕竟只占供水管网所有管道中的一小部分，其它的大量未发生事故的管段就成为了截尾数据，生存分析可以充分利用这些数据信息；
　　(3) 生存分析可以对多个危险因素同时进行分析，亦可对混杂因素进行控制。导致供水管网管道发生爆裂原因十分复杂，通常与多种因素相关，生存分析可以考虑这些相关因素，并对这些因素进行筛选，剔除其中影响程度小的因素后，建立爆管比例危险模型或LogT的位置－尺度模型。
　　目前我国管网运行管理科学水平相对较低，管道维护有效数据记录历时年限较短，相关信息记录收集指标过于简单，且以往的爆管分析通常只把分析对象局限于管网中爆管的管段，故用于分析数据在数量方面和质量方面都十分有限。实际上，那些从未爆裂过的管段数据也极具研究价值，也应列为爆管分析的研究对象，这样就能最大限度的扩展爆管分析对象，在一定程度上缓解了爆管分析数据数量不足的问题。
2.3 供水管道生存分析方法的选择
　　生存时间的分布是一般偏态的，不服从正态分布，常用指数分布、Weibull分布、gamma分布、logistic分布、对数正态分布等来描述。但是，对于一批未知寿命分布的总体趋势的生存数据，不易判断应该采用何种模型，一般可以直接采用非参数方法或半参数法。如果一批数据确实符合一定的参数模型，用参数方法即可得到较高的分析精度。
　　供水管道的生存分析既可以采用非参数方法绘制管道的生存曲线及寿命表，从管道使用时间角度对管道的生存趋势进行分析，也可以采用参数法建立管道生存分析模型。因为管道的生存时间除了与管道使用年限密切相关，还与诸多管道内部和外部因素（COX称之为协变量）相关，如土壤类型、环境压力等因素。因此，对某一组同管龄的每个管道而言，假定它们具有相同的生存函数，既仅用寿命表、用Ｋ-Ｍ估计就会带来较大的偏差，所以应同时考虑多个影响因素对管道生存时间的影响。
　　在爆管分析的国外研究中，生存分析的非参数法、参数法中COX模型、指数模型、威布尔模型以及LogT的位置－尺度模型均被采用过，其中以非参数法、指数模型和威布尔模型采用的相对较多^【3】。如果已知样本资料的生存时间服从某种特定的分布，如指数分布、威布尔分布等,可以用参数统计方法中相应的模型来确定其分布参数和各危险因素之间的定量关系。如果样本资料的生存时间服从某种特定的分布未知，可以采用Cox回归模型，该模型的优越性之一就是对基准生存分布没有特殊要求,所以称为半参数回归模型，在实用方面比其它参数回归模型更为灵活，能够迅速方便地提供影响预后的参考因素。
　　由于本研究的爆管生存数据样本量较少，不易判断服从何种分布，故采用非参数生存分析法进行分析。
2.4 供水管道非参数法分析实例
　　表1是某市爆管数据记录，经过数据整理，有效数据记录共计147条，且所有记录都是完全数据。

爆管数据记录　　　　　　 表1

爆管日期

管径

管材

管龄

安装日期

埋深

其它

2001.5.16

200

铸铁管

2

1999

0.6

水泥接口

2001.7.4

100

钢管

2

1999

0.6

腐烂

2002.2.20

100

钢管

3

1999

0.5

腐烂

2003.12.15

150

铸铁管

4

1999

0.8

环向断裂

2002.3.7

600

水泥管

4

1998

1.2

水泥接口

2002.11.18

150

铸铁管

4

1998

0.6

环向断裂

　　对以上数据进行生存分析，得到以下分析成果：
　　（1）寿命表法：按不同的管材进行分组、时间间隔为3年建立管道寿命表，估计不同管材管段的生存概率。因篇幅所限，仅列出铸铁管寿命表，见表2。

铸铁管道寿命表　　　　　　　　　　表2

生存时间分段

进入区间例数

期内截尾数量

历险例数

期内失效例数

失效概率

生存概率p

累计生存率s

概率密度

危险率

.0

105.0

.0

105.0

1.0

.0095

.9905

.9905

.0032

.0032

3.0

104.0

.0

104.0

6.0

.0577

.9423

.9333

.0190

.0198

6.0

98.0

.0

98.0

9.0

.0918

.9082

.8476

.0286

.0321

9.0

89.0

.0

89.0

4.0

.0449

.9551

.8095

.0127

.0153

12.0

85.0

.0

85.0

10.0

.1176

.8824

.7143

.0317

.0417

15.0

75.0

.0

75.0

22.0

.2933

.7067

.5048

.0698

.1146

18.0

53.0

.0

53.0

23.0

.4340

.5660

.2857

.0730

.1847

21.0

30.0

.0

30.0

12.0

.4000

.6000

.1714

.0381

.1667

24.0

18.0

.0

18.0

3.0

.1667

.8333

.1429

.0095

.0606

27.0

15.0

.0

15.0

3.0

.2000

.8000

.1143

.0095

.0741

30.0

12.0

.0

12.0

6.0

.5000

.5000

.0571

.0190

.2222

33.0

6.0

.0

6.0

1.0

.1667

.8333

.0476

.0032

.0606

36.0

5.0

.0

5.0

4.0

.8000

.2000

.0095

.0127

.4444

39.0

1.0

.0

1.0

1.0

1.0000

.0000

.0000

.0032

.6667

　　（2）乘积极限法（K－M法）
　　该方法只估计失效时间点的生存率或危险率。按管径进行分组，不同级别管径管道生存曲线如图2，不同级别管径管道危险曲线如图3；按管材进行分组，不同管材管道生存曲线如图4，不同管材管道危险曲线如图5；

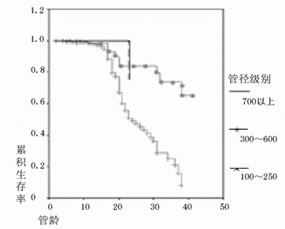
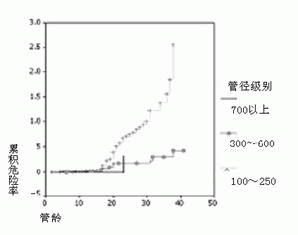
图2 按管径分组K－M法生存曲线

图3 按管径分组K－M法危险曲线

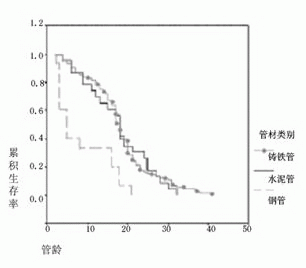
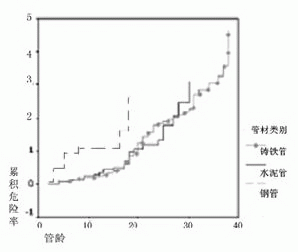
图4 按管材分组K－M法生存曲线

图5 按管材分组K－M法危险曲线

2.5 分析结论
　　（1）通过对不同的管材寿命表的比较可知，不同管材生存经历有所区别，水泥管与铸铁管相比，其生存概率下降较快。由表2铸铁管寿命表可见，铸铁管生存经历中管龄15－21年及36年后，爆裂危险率较高。对于不同的管材，铸铁管和水泥管的生存情况相近，钢管的情况较差，危险概率随时间上升最快，如图4、图5所示。
　　 （2）管径级别不同生存曲线有所差别，如图2、图3所示。从管道生存曲线和危险曲线上均可看出：对不同管径的管道，大管径管道（DN700以上）管道累计生存率下降最快、危险概率随时间上升最快，故危险程度最高，其次是小管径（DN100－DN250）的管道。
　　 （3）不同管材、不同管径的管道生存情况变化规律不同，如果样本量足够，应按管材、管径分组分别进行分析。由于观测量较少，一般采用K－M方法进行分析。K－M法一般适合用于小样本，适合于目前爆管维护数据量有限的情况。
　　 （4）非参数估计所得结果是跳跃性的，采用参数估计所得的结果可以是连续性的。

3 结束语

　　用生存分析法对供水管网爆管问题进行分析是探索爆管内在规律、解决爆管问题的一种新方法，可以为防治爆管决策的制定提供有效的依据。但不论是何种分析方法，其分析结果的准确性和有效性都极大的依赖于管道生存数据数量和质量。我国各供水管理部门应当重视管道维护运行数据的收集和整理工作，建立完整、严格、详细的相关数据库，为有效的决策分析提供丰富的数据资源。

【参考文献】

1. Jianhua Lei，.etc，Statistical Approach for Describing Failures and Life times of Water Mains，Wat.Sci.Tech. Vol.38.No.6.pp.209-217
2. Genevieve Pelletier,.etc, Modeling Water Pipe Breaks –Three Case Studies, Water Resources Planning and Management,2003,115-123
3. Yehuda Kleiner & Balvant Rajani, comprehensive review of structural deterioration of water mains: statistical models, Urban Water 3（2001）, 151-164 .
4. SPSS for Windows 统计分析软件，卢纹岱主编，电子工业出版社
5. 寿命数据中的统计模型与方法，J.F.Lawless著，中国统计出版社

论文作者：何芳
工作单位：广东佛山供水总公司调度中心；
地址：广东省佛山市禅城区同济西路16号；邮政编码：528000；
联系电话：0757－82187282；邮箱地址：hyhefang@tom.com